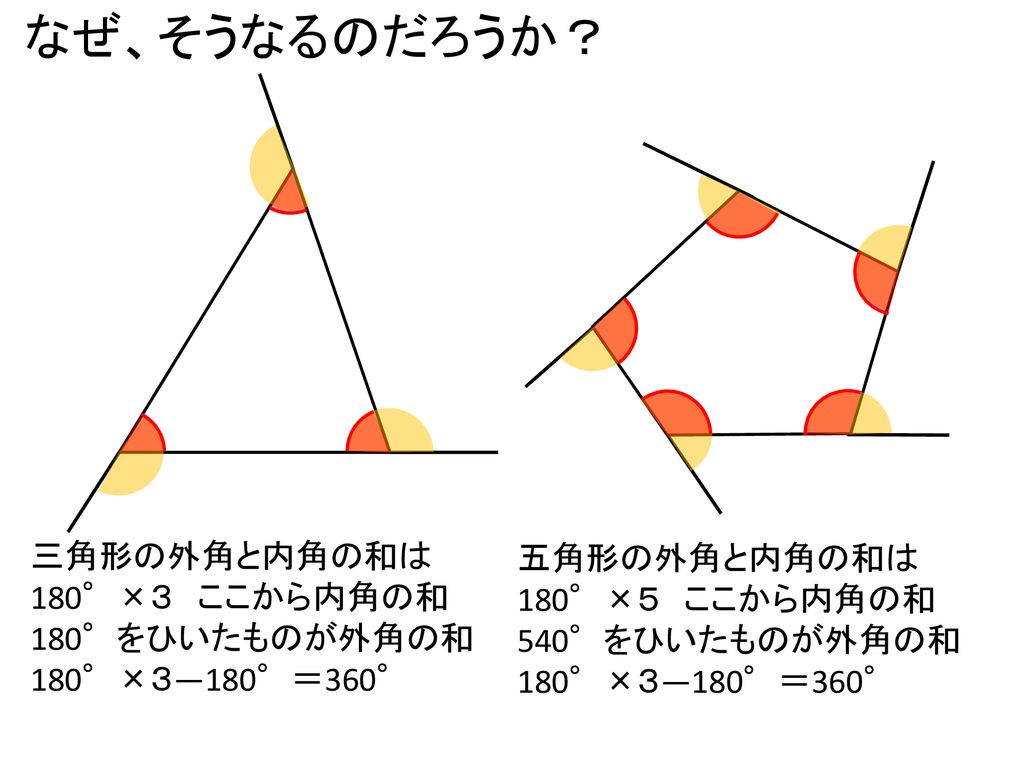
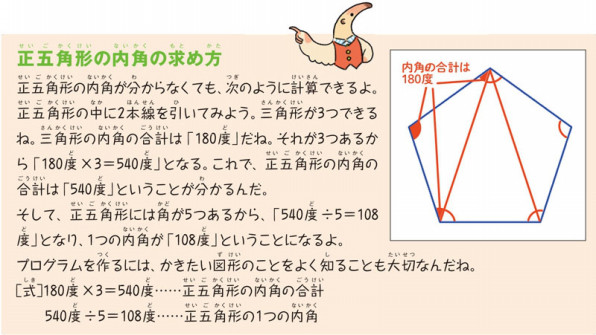
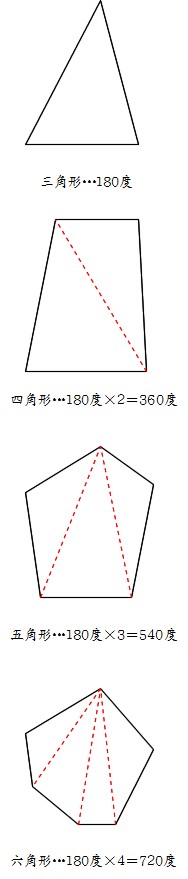
「五角形や六角形の内角の和を求 める方法を考えよう」 <五角形> ⇒三角形が3つできるから <六角形> 生徒は板書,あるいはノートに記入しながら発表する。 ⅰ.対角線が1本しか引けない。 対角線が引けていない四角形に目を向け させる。・多角形の内角の性質を調べる。 ・いろいろな多角形の内角の和を求 める。 思n 角形の内角の和が180°×(n-2)になること を帰納的、演繹的に導くことができる。 知多角形の内角を求めるいろいろな方法を理解し ている。 12年 多角形の外角|数学イメージ動画集|大日本図書 五角形の外角を全部合わせると 360° です。 同様に,他の多角形でも外角の和は 360° になります。 このことから,多角形の外角の和はいつも 360° になるということがわかります。 実施時期 2年生2
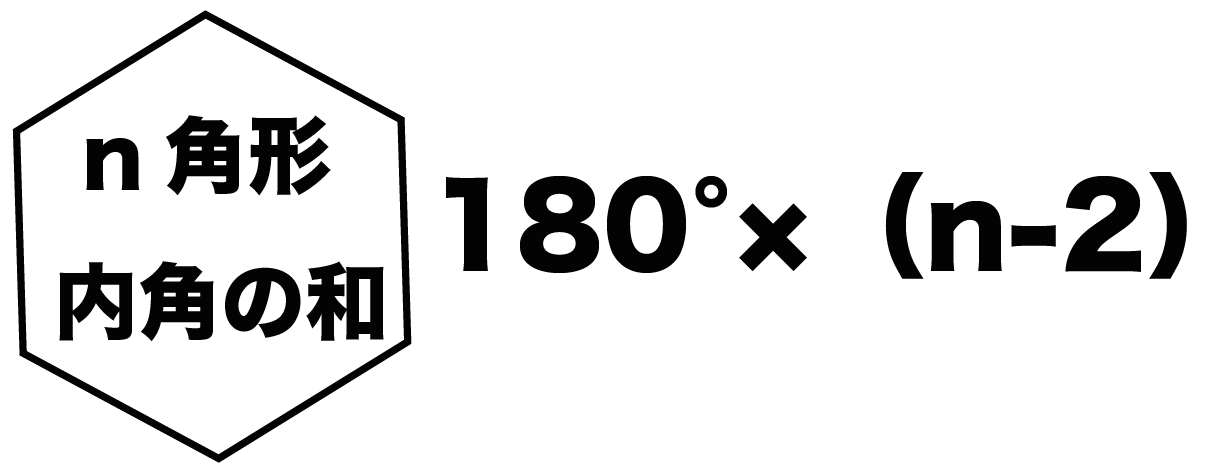
簡単公式 五角形の内角の和を3秒で計算できる方法 Qikeru 学びを楽しくわかりやすく
五角形の内角の和 求め方
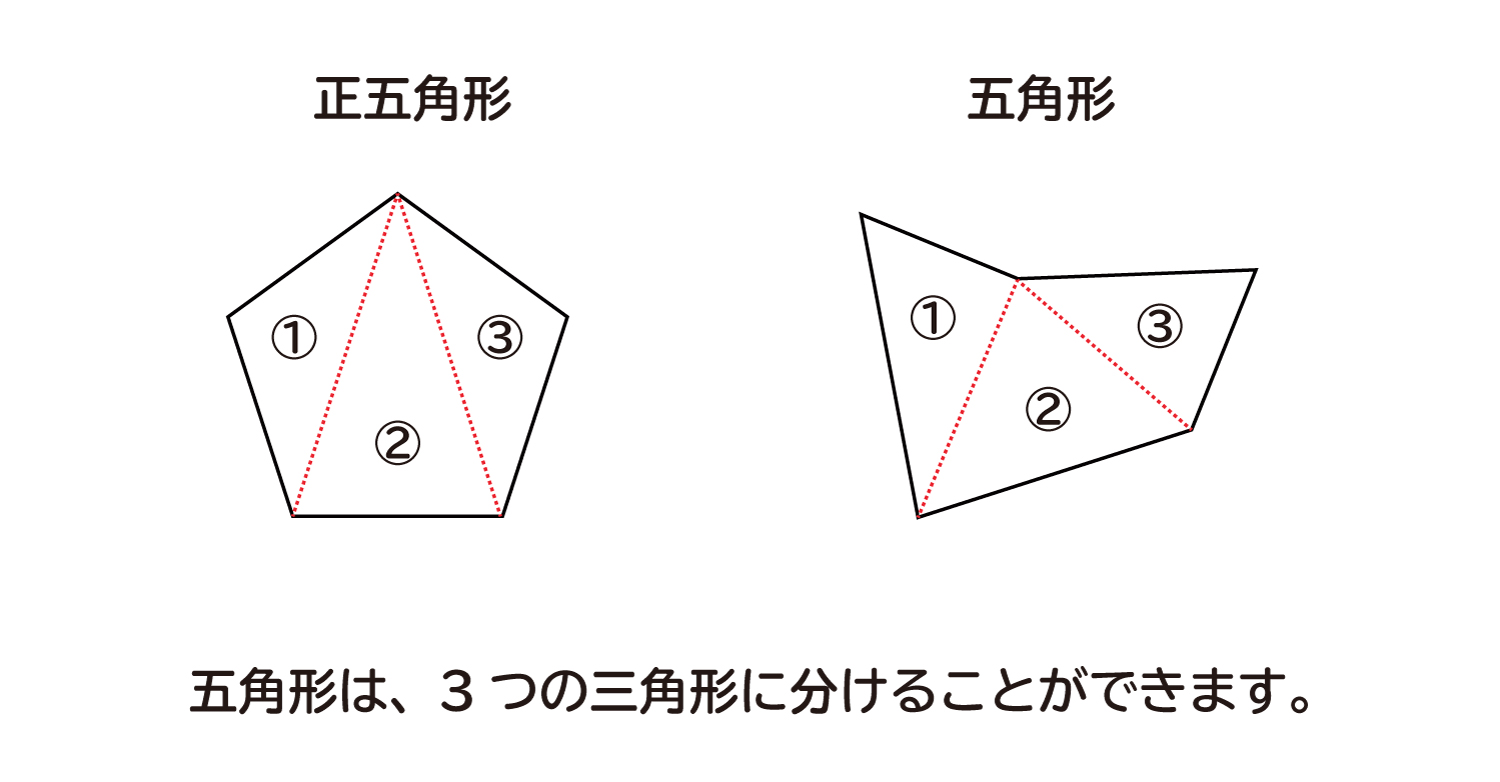
五角形の内角の和 求め方- 緑赤の内角の和は360°だよね?これって、結局、四角形の内角の和のことを言っているわけ! ほんじゃ次! 五角形の内角の和 答えは、540°なんだ。 同じように五角形の内角の和を考えてみる! 四角形と全く同じやり方で、五角形を三角形に分けてみよう!①三角形の内角の和が180°になる ①三角形の内角の和が,180°であ ①三角形や四角形の内角の和に ことや,四角形の内角の和が360° ることを帰納的に見出している。 ついて,筋道立てて考えよう になることを理解している。 ②四角形や五角形の内角の和を
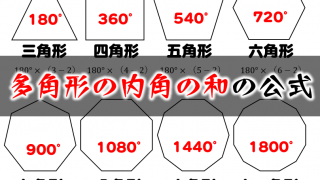



多角形 の内角の角度 計算ドリル 問題集 数学fun
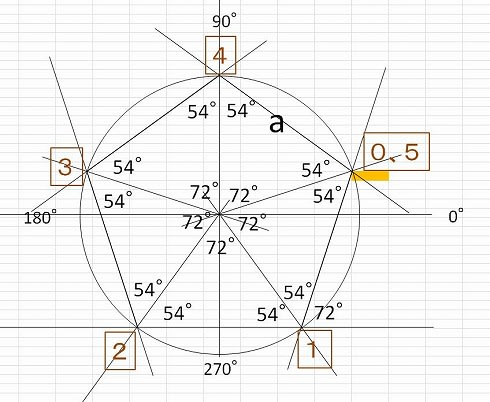
正五角形の作図 正五角形を自分で作図できるようになってみましょう。 正五角形とは, 定義①すべての辺の長さは等しく, 定義②すべての内角の大きさが等しい 図形の中で,辺および頂点の数が5個のもの。 ということにします。ただし,正5 2・ 「五角形」「六角形」「多角形」の・探究的な活動 ことを理解している。 4 定義を知る。 ・説明する活動 / ・ 五角形,六角形の内角の和を,三 8 角形に分割して調べ,多角形の内角 の和について表にまとめる。 ・ 多角形の内角の和のきまりを考え る。 五角形の内角の和は「三角形の内角の和(180°)」を3倍した 180°×3 = 540°
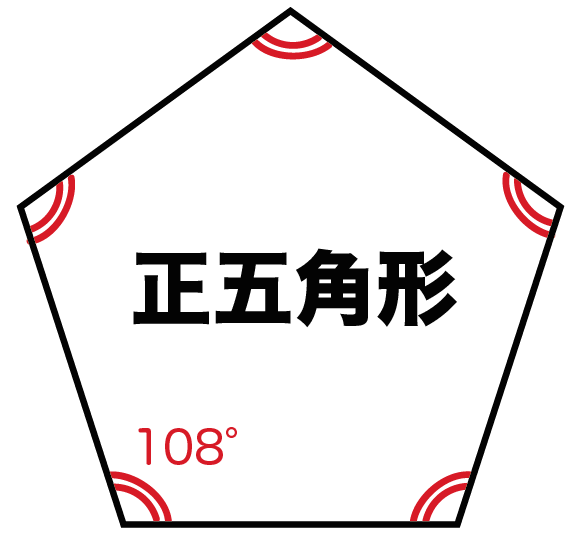
五角形の外角の和を,次のようにし て求めた。〔 〕にあてはまる数を書き なさい。 確認問題 1 a x 63ß 70ß x 110ß 150ß 2 s 五角形 六角形 七角形 八角形 頂点の数 5678 1つの頂点から 出る対角線の数 2 三角形の数 3 内角の和 180ß*3 =540ß 3 内角 外角 d さっそく、正五角形の内角を計算してみよう! 正五角形は頂点が5つあるから、 さっきの公式のnに「5」をいれるだけでいいんだ。 すると、 180 × (n2)/n = 180×(52)/5 = 108° になるね。 つまり、 正五角形の内角の大きさは「108°」ってことさ。 くそ便利でしょ??^_^三角形から四角形(3〜4辺)まで、 五角形から六角形(5〜6辺) 内角の総和に180°を加算する。 このルールは数式として書くことができます: (n2)×180° ここで、n =ポリゴンの辺の数。 したがって、六角形の内角の合計は、次の式を使用して求められます。
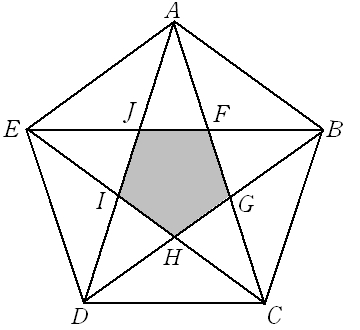
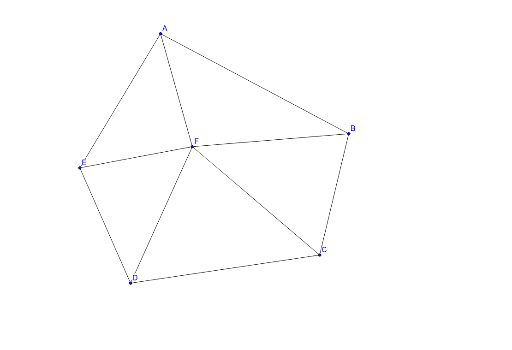
Afj, bgf,等の5つの三角形の内角の和から,五角形の外角の和2つ分を引いて, 180×5-360×2 =180° 外側の五角形から付け足した三角形5つ分を引き,内側の五角形をたすと, 180×(5-2)-180×5 +180×(5-2)=180°・5つの頂角を1つの三角形の内角に集める。 ・五角形の内角・外角を利用する。 ・その他 ・自分の解き方を説明している。 ・友だちの解き方を聞き,納得したり,新しい方法を考えている。 ・180度と答えた生徒が多い。・五角形の場合:n=5 ・内部に作成できる三角形の数:n-2=5-2=3個 540度 どうですか?五角形の内角の和は540度で間違いないですよね? したがって、 となるのです。これが 公式 ですよ^^



茗渓予備校 科目別データベース




8 Times31 Descubre Como Resolverlo En Qanda
後悔(五角形の内角の和) 1332 テーマ: 5年生「図形」12 三角形や四角形の内角の和をまとめ,多角形の内角について考えていきます。 まず前時に明らかになった「三角形の内角の和は180°」と「四角形の内角の和は360°」ということを確認した後, 「180とか360とか中途半端だよねえ。 どうせなら100や0なら覚えやすいのにね。(2)主眼 星形五角形の内角の和を既習事項を使って、求めることができる。 (3)展開 学 習 活 動 指 導 および 支 援 時間 備考・ICT機器 評価(方法) 1.星形五角形の内角の 和が何度になるか、 予想し,調べる。 (本時のめあて) 2.自分の考えでる。星型五角形を2つの三角形ACDと三角形B FEに分ける。それらの内角の総和360°から, FCDの内角の和180°を引き,星型五角形の 内角の和180°を求めることができる。 f ウ 五角形の外角の和を利用する 図のように,星型五角形の5つの角をそれぞれ



1




多角形 四角形 五角形 六角形 の内角の和の公式 問題の解き方 数学fun
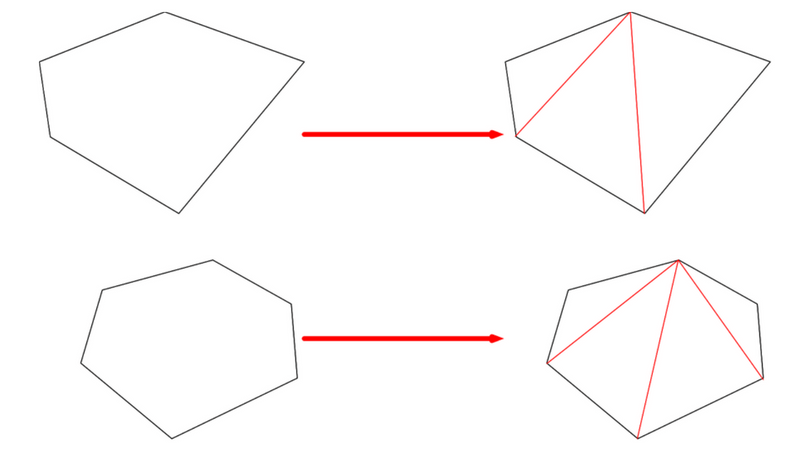
内角の和は 180°×2=360° となった。 五角形の場合も同じように考えると、 3 つの三角形がで きるので、内角の和は 180°×3=540° 六角形の内角の和は、 180°×4=7° n 角形の場合を考えると、一つの頂点から対角線を引い五角形の内角の和: 540° 540 ° 六角形の内角の和: 7° 7 ° ・・・ n角形の内角の和: 180°× (n−2) 180 ° × ( n − 2 ) この公式は覚えやすいので暗記してもいいのですが、簡単に導出できるため、わざわざ覚える必要もありません。 ではどのようにこの公式を導出するのか、なぜ内角の和が「 180°× (n −2) 180 ° × ( n − 2 ) 」になるのか、 (n−2) ( n −五角形の場合はそれが5つあるので、五角形の外角と内角の和が900°であることが分かっています。 一方で、内角の和は先ほど求めたように、 180°×3=540° ですね。
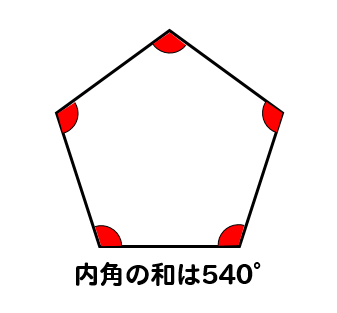



正多角形の1つの内角 外角を求める方法を問題解説 数スタ



多角形の外角の和 凹型四角形の角 星形五角形の内角の和 Ppt Download
正五角形の一つの内角の大きさ )と一定な五角形である。辺の長さを a とすると 面 内角1つ分の大きさは \LARGE {=108° さっそく、正五角形の内角を計算してみよう!星形多角形の内角とは,多角形 の各辺の延長線でつくられた, 鋭角のみをいいます。 ∠a+∠b+∠c+∠d+∠e を 星形五角形の内角といいます。 星形多角形の内角 星形多角形 2 星形五角形の角の和を求めよう(∠a+∠b+∠c+∠d+∠e)内角の和と三角形の関係は?1分でわかる和の値、証明、外角との関係 外角と内角の違い 外角と内角の違いを下記に示します。 外角 ⇒ 多角形の外側にできる角 内角 ⇒ 多角形の内側にできる角 下図をみてください。三角形の内角と外角を示しました。




内角の和の公式 内角の和が1800 の多角形は何角形 中学や高校の数学の計算問題




無料 中2数学 標準問題 解答プリント 223 図形3 多角形の角
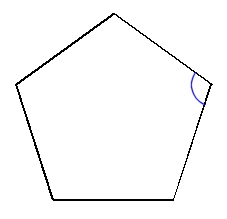
右の表のように,n角形を三角形に分けると, 内角の和は 180°×(n−2) になる. ≪例≫ 三角形の内角の和は180° 四角形の外角の和も360° 五角形の外角の和も540°四角形、五角形、六角形・・・十角形なんかもそうだね。 三角形の内角の和 (角度を全部たしたもの)が 180° になるのは知っているよね。 では、角が多い、多角形の内角の和はどうなるんだろう。 正五角形の1つの内角の大きさは、何度か。 内角で求めるか、外角で求めるかの2パターンある。 内角で求める解き方 1つの角度を聞いているので、五角形の内角の和÷5 540÷5=108 外角で求める解き方 360÷5=72 =108 図は、ある正多角形の一部である。



2



多角形の内角の和 は何度なのか を説明します おかわりドリル
五角形の外角の和を考えてみよう。 の和は180° AからEまでの全ての頂点の内角と外角を足す と、 ←画像をクリック! 五角形の内角の和は概要 (表示しない) 中学校数学第2学年「平行と合同」を学習後、課題学習として「星形5角形の内角の和」の授業を実施しました。 説明方法が何通りもあること、また、視覚的に説明した方が理解しやすいと考え、コンピュータを利用しました。 事前に生徒の考えを予想し教材として作成し、パソコン上で、角を移動させ、視覚的に理解できるよう配慮しました。星形五角形の印を つけた5つの 角の和は何度でしょう。 どんな星形五角形でも印をつけた5つの角の和は180°に なる。その理由をできるだけ多くの方法で説明してみよう。 ①ブーメラン型の図形 の角度を利用 ②補助線を引く⇒三角形 の内角の和



3




多角形 の内角の角度 計算ドリル 問題集 数学fun
正解です 正解は 108°です。 タヌキ 正5角形の内角の和を計算すると 5角形は三角形3つに分けることができるから 180×3=540°となります。 キツネ 正5角形は5つの等しい内角でできていて この5つの角度の和は、540°だから、 1つの角は 540÷5=108°と計算できます。 五角形の外角S:四角形,五角形の内角の和は,360度,540度になりそう。 学習課題(5時間目) 四角形,五角形の内角の和を調べていくことでどのようなことがわかるだろうか。 多角形の角 となることがわかる。 次時に繋げる「Whatifnot」正五角形の1つ分の外角は72°となるので 内角1つ分の大きさは $$\large{=108°}$$ となります。 同様に 正六角形の1つ分の内角は\(=1°\) 正八角形の1つ分の内角は\(=135°\) 正九角形の1つ分の内角は\(=140°\) 正十角形の1つ分の内角は\(=144°\)



正多角形の内角を4秒で計算できる公式 Qikeru 学びを楽しくわかりやすく
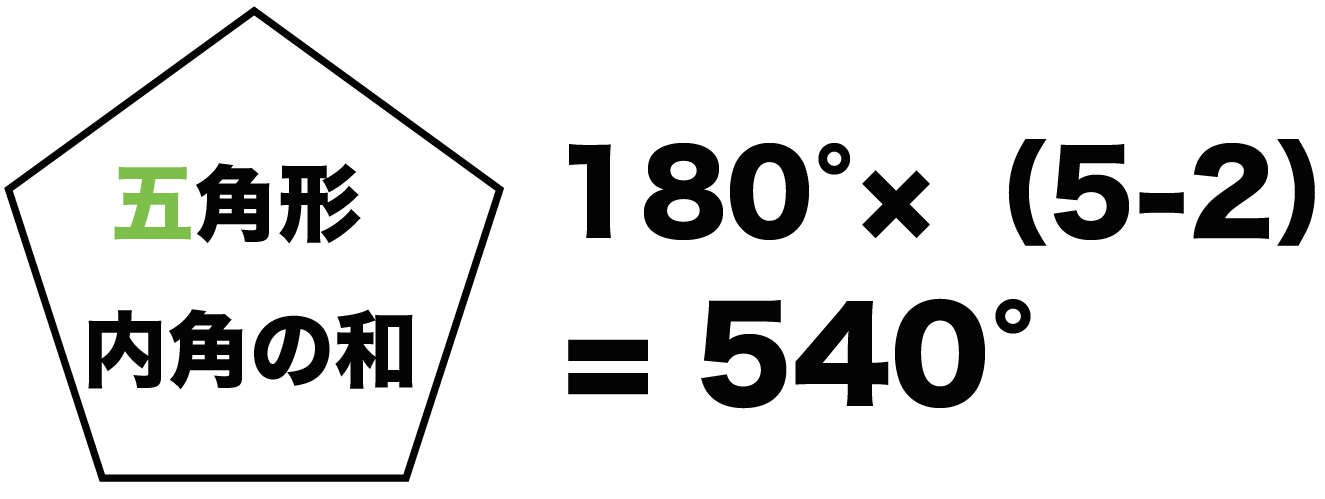



簡単公式 五角形の内角の和を3秒で計算できる方法 Qikeru 学びを楽しくわかりやすく
「五角形」、「六角形」や「多角形」 の用語とその定義を理解し、それぞ れの形の内角の和を求めることが できる。 ・ 五角形の内角の和を工夫して求 め、540°であることを説明する。 ・ 多角形の内角の和を表にまとめ る。 児童が説明する算数的活動



直角正五角形
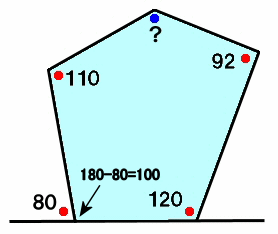



五角形の内角




飯塚 弘貴 Hiroki Iizuka V Twitter 正解 7度 下図でa B C Dなので 印をつけた角の和は五角形と三角形の内角の和に等しい よって540 180 7度となる




簡単公式 五角形の内角の和を3秒で計算できる方法 Qikeru 学びを楽しくわかりやすく




数学 中2 51 多角形の内角と外角の和 基本編 Youtube



1
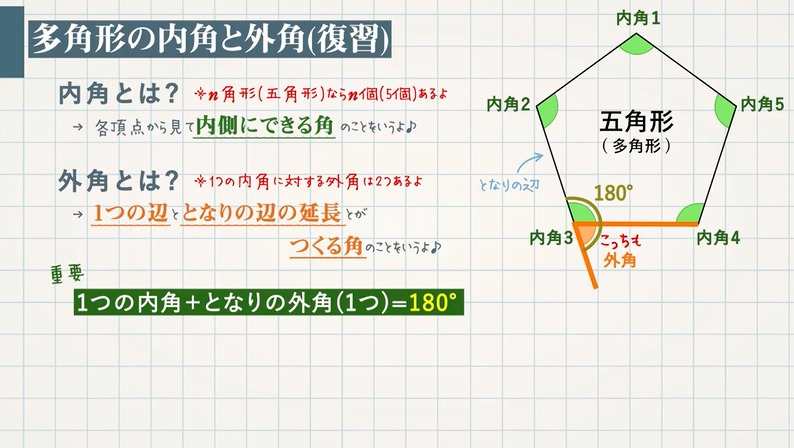



三角形の内角と外角の性質 教遊者




十五角形 Wikipedia



ペンタゴンの秘密 正五角形の謎を解く 空間情報クラブ 株式会社インフォマティクス




中学数学 五角形の内角 Youtube



n角形 多角形 の内角の和の求め方




この問題の答えはイなんですけど どうしてそうなるのかが分かりません Clear



五角形の内角の和の求め方 久保塾 今治市の学習塾




中学2年生 覚えておくと便利な角度の関係 公式 個別進学教室マナラボ受験 教育情報サイト
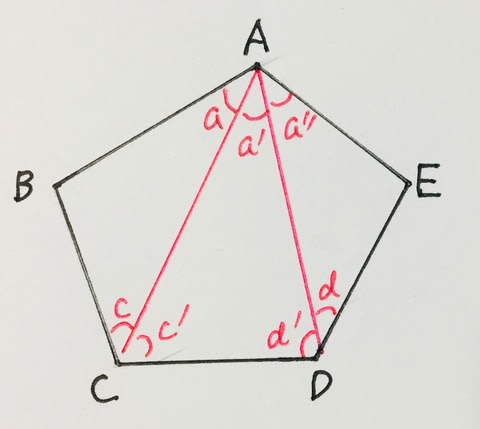



多角形の内角の和 五角形 Takapの数学日記
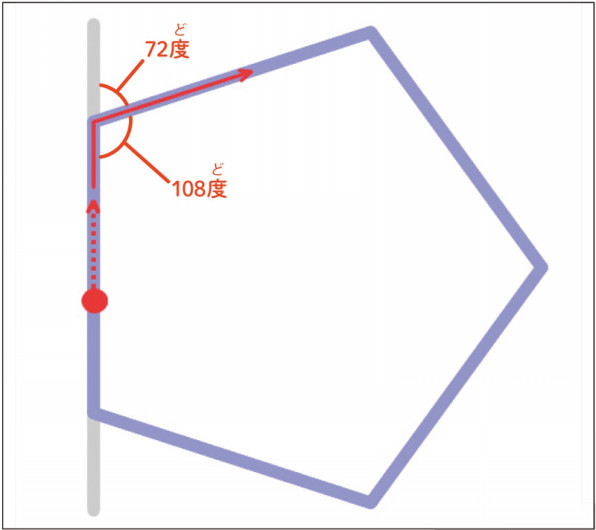



スクラッチ入門 16 正五角形をかいてみよう はじめる 楽しむ プログラミング こどもプログラミング教育のツボ ジャムハウス



この方法で星型五角形の五つの内角の和の求め方をおしえてください A Yahoo 知恵袋



Math 多角形の内角の和 働きアリ




8 2 Descubre Como Resolverlo En Qanda




スタディピア 平面図の内角の和



1
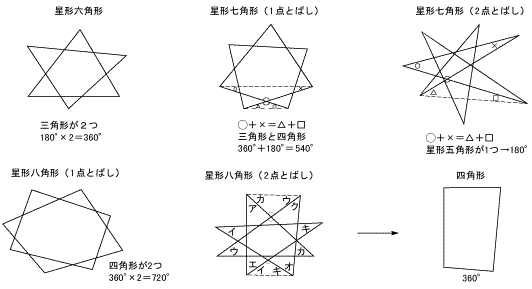



課題学習の指導 数学
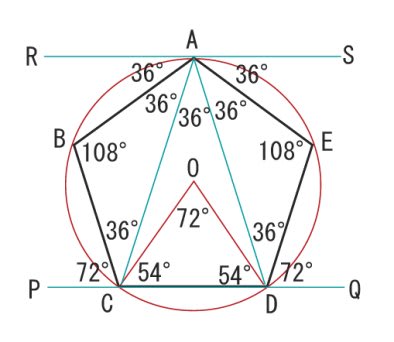



正五角形というだけで 分かる角度は 名寄 算数数学教室より
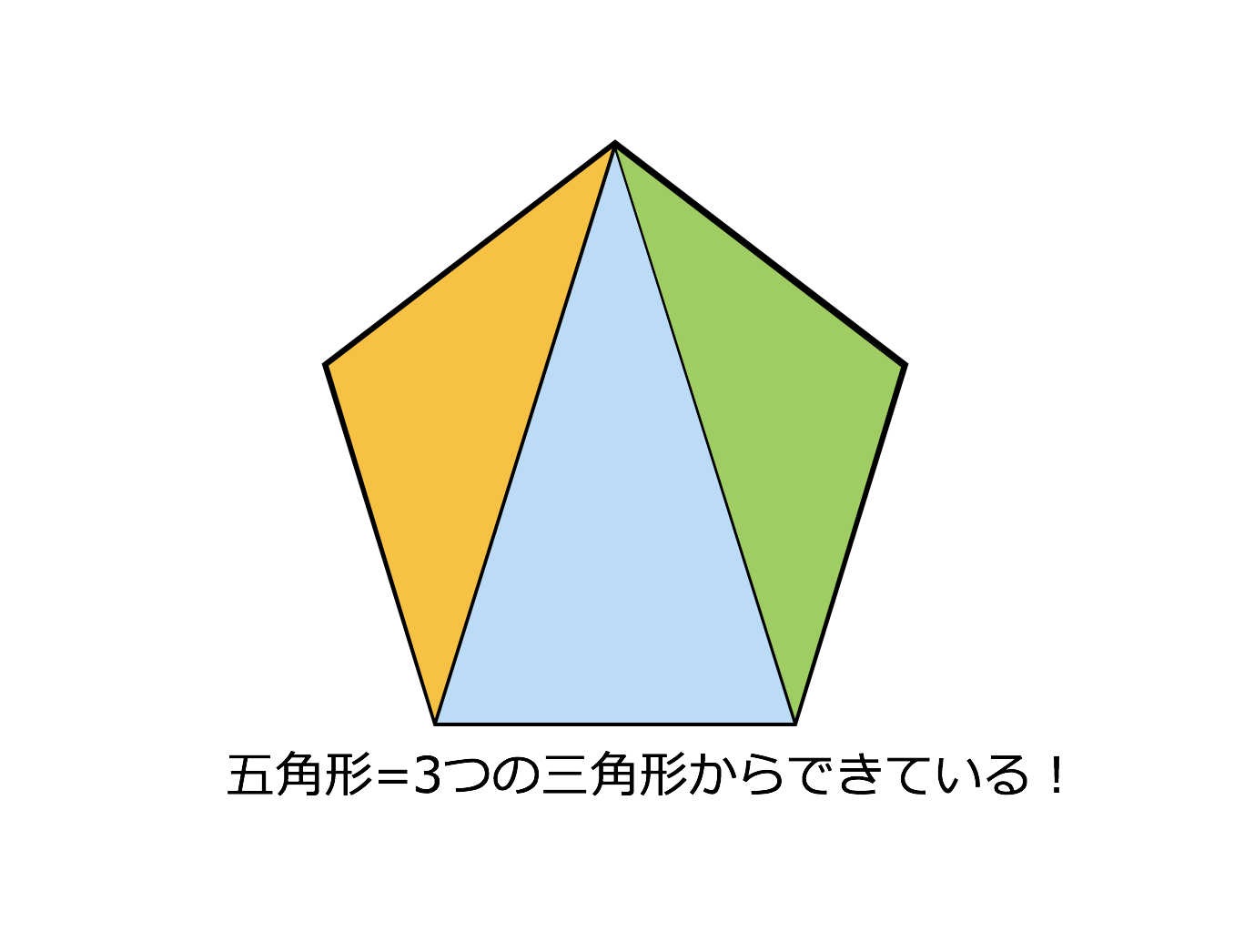



3分で分かる 多角形の内角の和の求め方 公式の証明などをわかりやすく 合格サプリ




中学数学 平行と合同 多角形と角 星形五角形の内角の和 Youtube




五角形 Wikipedia



スクラッチ入門 16 正五角形をかいてみよう はじめる 楽しむ プログラミング こどもプログラミング教育のツボ ジャムハウス




多角形の内角の和の公式を3通りの方法で証明する 具体例で学ぶ数学




多角形の内角の和と外角の和 三角形や四角形 五角形の角度 リョースケ大学



三角形の内角の和が180度である理由と外角の和や多角形の公式 まぜこぜ情報局



五角形の内角の和 Geogebra




多角形の内角の和 外角の和の公式 数学fun




中学数学 平行と合同 多角形と角 星形五角形の内角の和 Youtube



ペンタゴンの秘密 正五角形の謎を解く 空間情報クラブ 株式会社インフォマティクス




多角形の内角の和 算数の公式覚えてますか



正五角形の内角 外角



Math 多角形の内角の和 働きアリ



ペンタゴンボールの型紙 エクセルvbaで正五角形を作図してみましたpart 2 日だまりのエクセルと蝉しぐれ




内角の和 算数用語集




スクラッチ入門 16 正五角形をかいてみよう はじめる 楽しむ プログラミング こどもプログラミング教育のツボ ジャムハウス



多角形とは 外角 内角の和 面積 対角線の本数の公式と求め方 受験辞典




多角形とは 内角の和の求め方を簡単に解説 高校生向け受験応援メディア 受験のミカタ




多角形の性質 第2回 多角形の内角の和の求め方 算数パラダイス




正十五角形の1つの内角の大きさを求めなさい Clear




正五角形に付随する角度と黄金比の関係 萌えとかプログラミングとか




中学数学 三角形と角 五角形の内角 Youtube



数学得意な方お願いします 正五角形の1つの内角は何度になりますか その角度を求 Yahoo 知恵袋
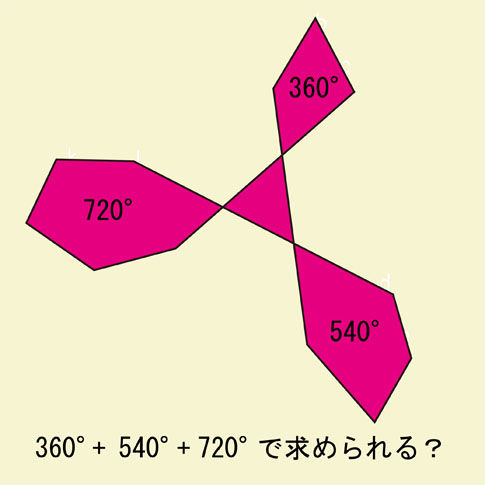



12個の角の和を求められますか 油断大敵を地で行く問題 秒刊sunday



五角形の内角の和について 五角形を三角形に分けて考えるとき 写真の中の上と下 Yahoo 知恵袋




多角形の内角の和 は何度なのか を説明します おかわりドリル
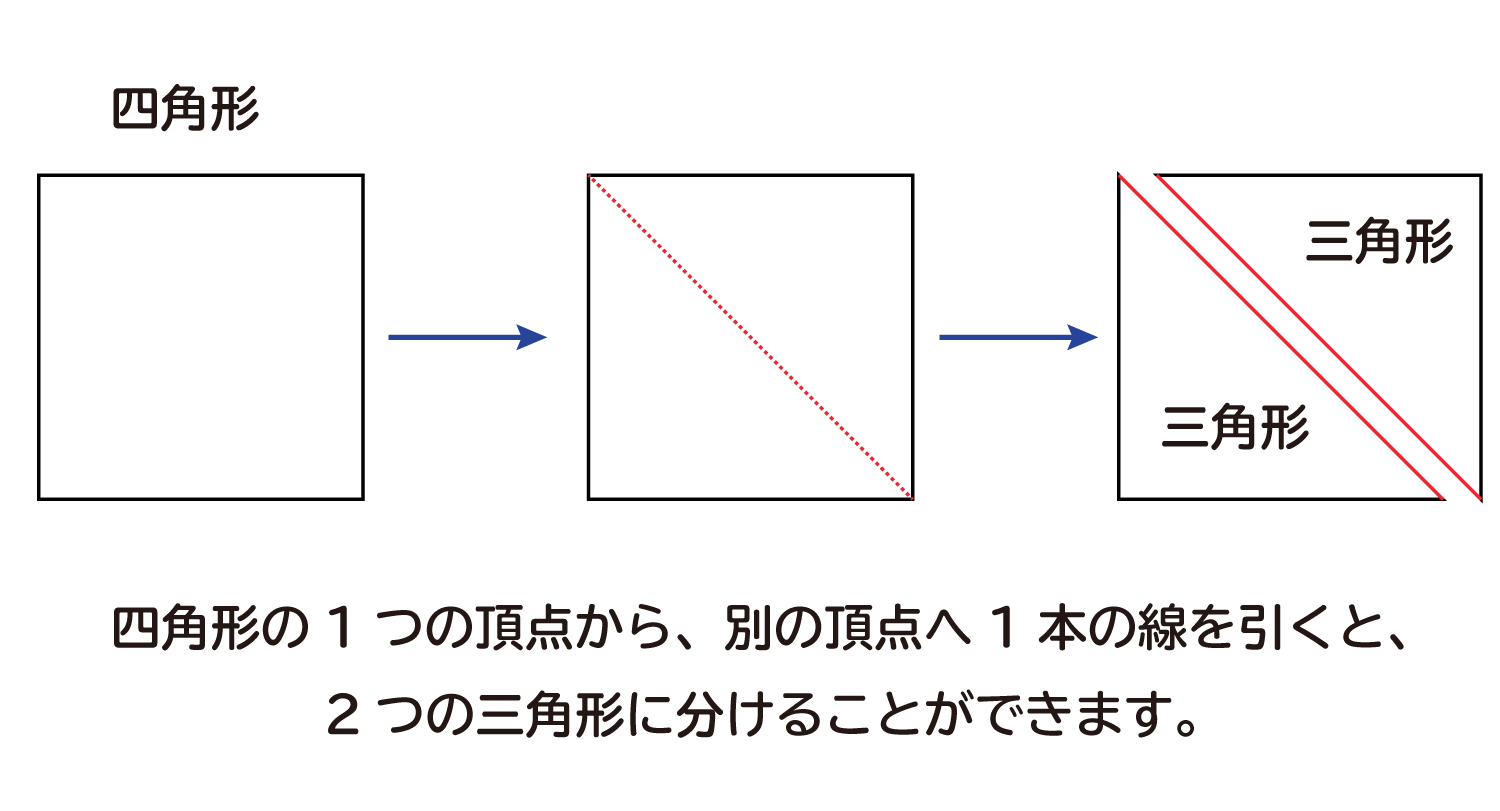



多角形の内角の和 は何度なのか を説明します おかわりドリル
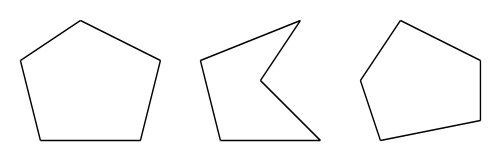



5角形の内角の和




正多角形の内角と外角の大きさ 具体例で学ぶ数学



多角形の内角の和 勉強ナビゲーター
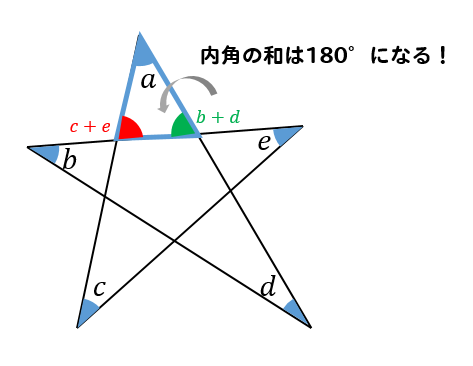



星形の角度 内角の和の求め方を問題解説 数スタ



多角形の内角と外角 思考力を鍛える数学
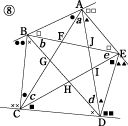



課題学習の指導 数学




o Zazbavb3a A 180nn Descubre Como Resolverlo En Qanda



図形 正五角形の分解 父ちゃんが教えたるっ




簡単公式 五角形の内角の和を3秒で計算できる方法 Qikeru 学びを楽しくわかりやすく




正多角形の内角を4秒で計算できる公式 Qikeru 学びを楽しくわかりやすく




なぜ 求める角の大きさの和が星型の内部の五角形の内角の和に等しくなるのでしょうか Clear



南山中学女子部過去問題演習




五角形の内角の和 ワークシート スクールプレゼンター教材共有サイト スクプレ道場




正多角形の 内角が あっという間に分かる術 名寄 算数数学教室より




3分で分かる 多角形の内角の和の求め方 公式の証明などをわかりやすく 合格サプリ



正五角形の作図法 数理女子



中学二年生の星形五角形の内角の和の求め方を教えてください 星 Yahoo 知恵袋
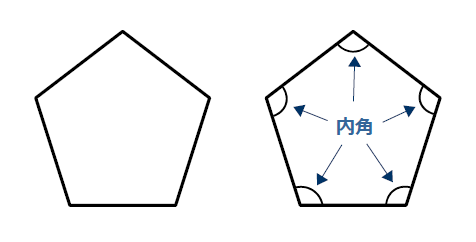



内角 ゆるゆるプログラミング




多角形の内角の和の公式を3通りの方法で証明する 具体例で学ぶ数学
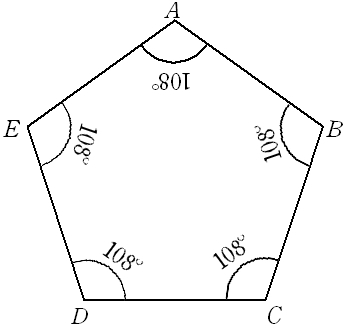



茗渓予備校 科目別データベース




多角形の内角の和 外角の和は 正多角形の内角の求め方は 証明や問題をわかりやすく解説 遊ぶ数学



正五角形ではない ホームベースのような五角形の内角の和を求める式が 180 5 Yahoo 知恵袋




図形の名前で 書かなくても分かる 数値とは 名寄 算数数学教室より 算数 数学教室 数学
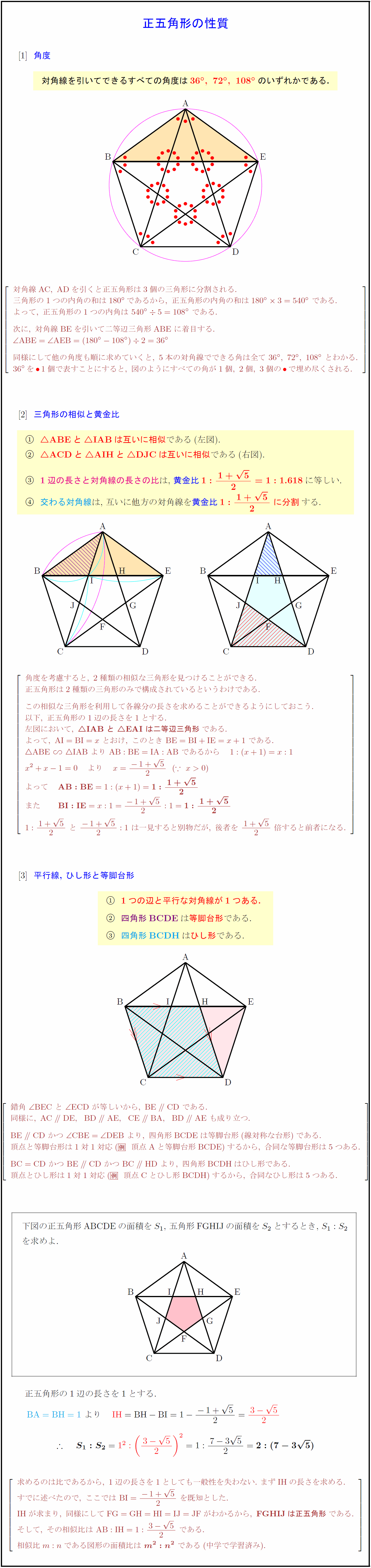



高校数学a 正五角形の性質 三角形の相似 黄金比 等脚台形 ひし形 受験の月




課題学習の指導 数学




中学2年の数学 動画 多角形の内角と外角の和 計算編の問題 19ch




8 2 Descubre Como Resolverlo En Qanda




小学5年生 正多角形 算数 Active Learning 学院



南山中学女子部過去問題演習




簡単公式 五角形の内角の和を3秒で計算できる方法 Qikeru 学びを楽しくわかりやすく




多角形の内角の和の求め方をイチから解説するぞ 中学数学 理科の学習まとめサイト
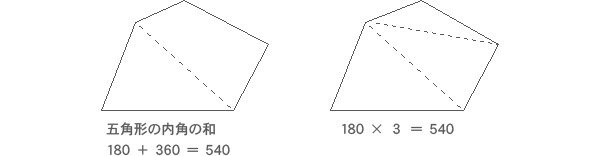



重なる形と図形の角を調べよう 第5学年 小学校 算数 My実践事例 日本文教出版




多角形の外角の和 凹型四角形の角 星形五角形の内角の和 Ppt Download




中2数学 正多角形の外角の大きさが3秒でわかる公式 Qikeru 学びを楽しくわかりやすく



中二 五角形の内角の和の求め方 をアップ 久保塾 今治市の学習塾
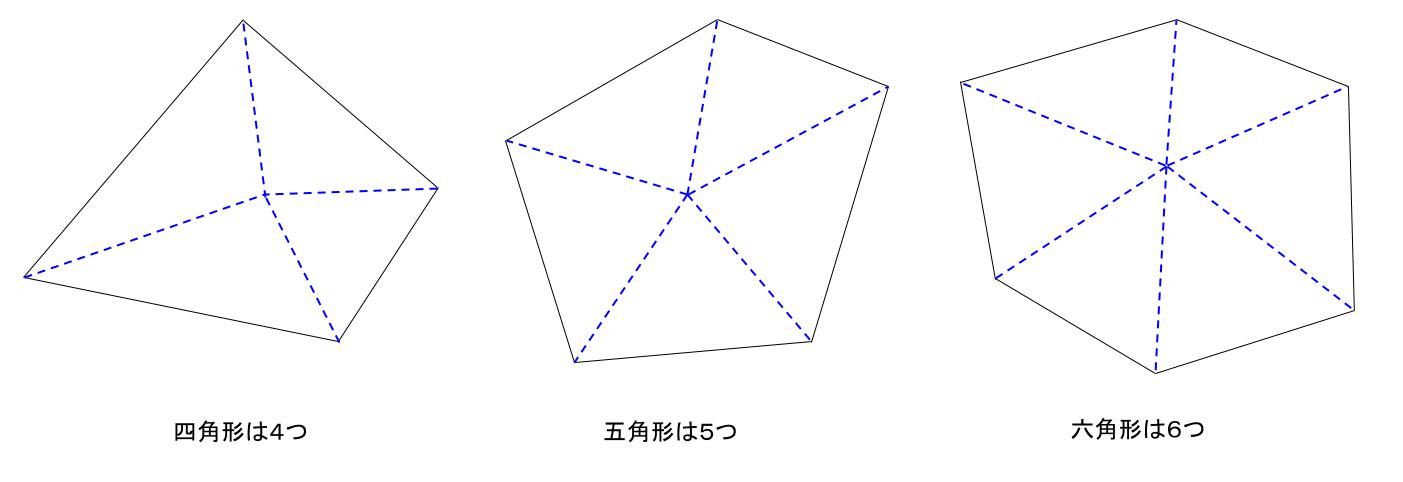



中学数学 多角形の内角 外角 中学数学の無料オンライン学習サイトchu Su




多角形の内角の和 は何度なのか を説明します おかわりドリル




小学校5年 算数 正多角形の角の大きさ Youtube




無料 中2数学 発展問題 解答プリント 図形4 三角形の合同条件


